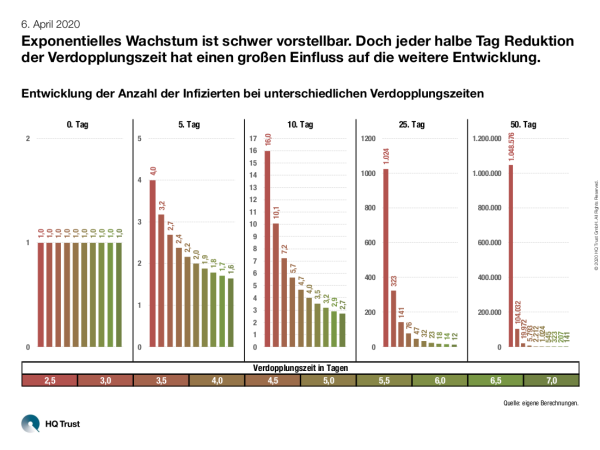
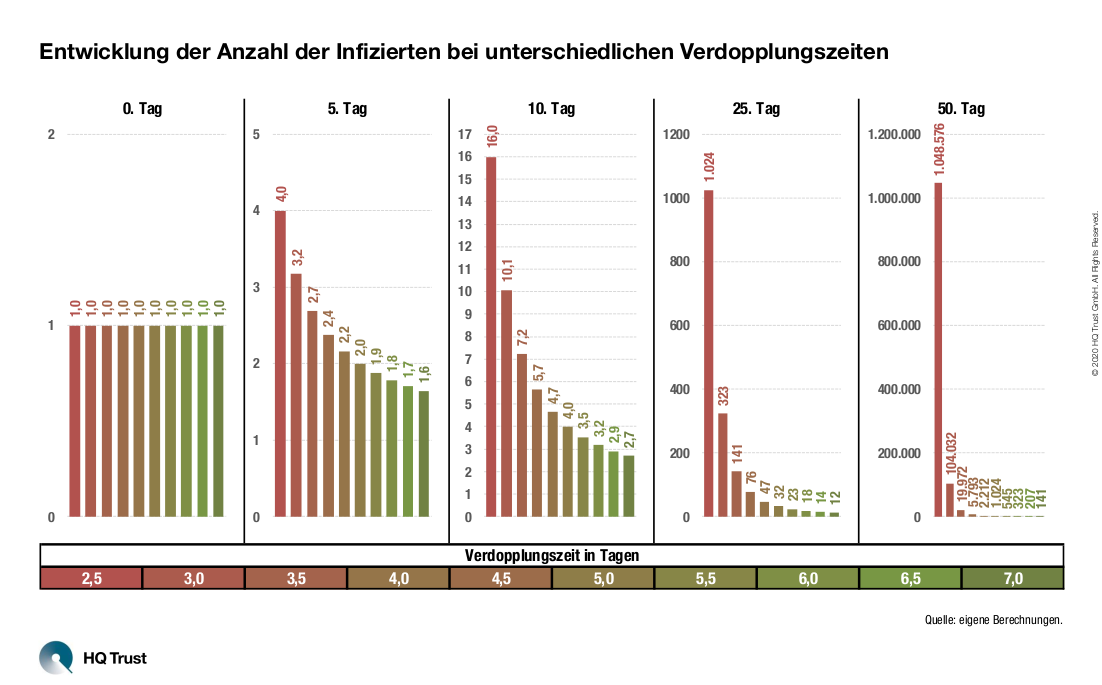
Bei exponentiellem Wachstum denken auch Anleger zuerst an den Matheunterricht: Da ging es um Reiskörner auf einem Schachbrett oder das Blatt Papier, das – oft genug gefaltet – bis zum Mond reicht. Also nichts, was mit dem realen Leben zu tun hat. „In der Coronakrise spielt es eine wichtige Rolle“, sagt Sven Lehmann von HQ Trust. „Selbst eine geringe Reduktion der Verdopplungszeit hat einen enormen Einfluss auf die Zahl der Infizierten.“
Um die Auswirkungen unterschiedlicher Verdopplungszeiten zu veranschaulichen, hat der Mathematiker und Fondsmanager ausgerechnet, wie sich eine Reduktion bei der Verdopplungszeit auf die Anzahl der Infizierten auswirkt. Seine Berechnung startet an Tag 0 mit einem Infizierten. Sven Lehmann unterstellt eine konstante Verdopplungszeit, die von 2,5 bis zu 7 Tagen reicht.
Exponentielles Wachstum ist schwer vorstellbar. Doch jeder halbe Tag Reduktion der Verdopplungszeit hat einen großen Einfluss auf die weitere Entwicklung.
- „Exponentielles Wachstum ist für uns schwer vorstellbar, da es im normalen Leben selten und dann nur kurz vorkommt, weil es dann schnell unvorstellbare Ausmaße annimmt.“
- „Derzeit tritt es im Zusammenhang mit der Ausbreitung des Coronavirus auf. Es geht um Fragen wie: Mit welchem Wachstum breitet es sich aus? Welche Zeit vergeht, bis sich die Anzahl der infizierten sich verdoppelt hat?“
- „In den ersten Tagen sind die Unterschiede klein, doch schon am zehnten Tag werden die Unterschiede größer: Bei einer Verdopplungszeit von 2,5 Tagen gibt es bereits 16 Infizierte. Bei einer Verdopplungszeit von drei Tagen sind es nur zehn oder 37 % weniger, bei sieben Tagen Verdopplungszeit lediglich drei Erkrankte (67 % weniger).“
- „Am 25. Tag sind die Unterschiede bereits enorm groß. Bei einer Verdopplungszeit von 2,5 Tagen gäbe es 1024 Infizierte, bei drei Tagen Verdopplungszeit wären es 323 oder 69 % weniger. Bei sieben Tagen wären es nur zwölf (99 % weniger).“
- „Kurz gesagt: Es kann enorme Auswirkungen haben, die einschlägig bekannten Hygiene- und Verhaltensregeln zur Vorbeugung von Infektionen zu befolgen. Bleiben Sie gesund!“
Und hier kommen noch die Lösungen der beiden „Schulaufgaben“.
Beim Schachbrett geht es darum herauszufinden, wie groß die Zahl der Körner wird, wenn auf jedem Feld die doppelte Anzahl Reiskörner liegen wie auf dem vorangehenden. Das bedeutet: Auf dem ersten Feld liegt ein Reiskorn, auf dem zweiten Feld zwei, auf das dritte Feld kommen vier Reiskörner … und so weiter bis zum 64. Feld. Auf dem liegen rund 9,2 Trillionen Reiskörner – mit einem Gewicht, das in etwa dem fünffachen Gewicht des Bodensees entspricht.
Bei der Rechenaufgabe mit dem Blatt Papier soll herausgefunden werden, wie oft es gefaltet werden muss, um (rein theoretisch natürlich) bis zum Mond zu reichen. Hier verdoppelt sich bei jedem Faltvorgang die Dicke. Unterstellt wird, dass das Blatt zu Beginn 0,099 Millimeter dick und der Mond gut 380.000 Kilometer entfernt ist. Beim 42. Falten hätten Sie den Mond erreicht. Zur Sonne geht es dann schnell: einfach nur noch neunmal weiterfalten.
Die Übersicht unserer Chart of The Week-Veröffentlichungen finden Sie hier. popup:yes
Bitte beachten Sie:
Die Vermögensanlage an den Kapitalmärkten ist mit Risiken verbunden und kann im Extremfall zum Verlust des gesamten eingesetzten Kapitals führen. Die Wertentwicklung in der Vergangenheit ist kein Indikator für die Wertentwicklung in der Zukunft. Auch Prognosen haben keine verlässliche Aussagekraft für künftige Wertentwicklungen. Die Darstellung ist keine Anlage-, Rechts- und/oder Steuerberatung. Alle Inhalte auf unserer Webseite dienen lediglich der Information.